IEE.OPT

Das Optimierungsmodell, welches im als Grundlage für die optimierte Netzausbauplanung als auch für die optimierte Netzbetriebsführung dient, basiert auf einer schnellen entkoppelten Leistungsflussberechnung, welche effizient hinischtlich der Berechnungszeiten sowie robust hinischtlich der Konvergenz ist. Das Optimierungswerkzeug und damit auch das Optimierungsmodell ist vor allem für die Hoch- und Höchstspannungsebene geeignet, da mit der schnellen entkoppelten Leistungsflussberechnung keine Berechnung der Netzknotenspannungsbeträge möglich ist. In diesen Spannungsebenen sind die notwendigen Anpassungen wie beispielsweise der Netzausbau vorallem getrieben ist durch die maximale Stormtragfähigkeit und nicht durch Spannungsbandverletzungen.

Zielfunktionen der optimierten Netzausbauplanung und der optimierten Netzbetriebsführung des Optimierungswerkzeugs:

Nachfolgend sind die Nebenbedingungen der optimierten Netzausbauplanung dargestellt:

Die erste Nebenbedingung, welcher im Rahmen der optimierten Netzausbauplanung verwendet wird, ist die Leistungfllussnebenbedingung.  Dabei entspricht P_ij dem Wirkleistungsfluss über einem Zweigelement, x_ij entspricht der Reaktanz basierend auf dem Entscheidungsvektor u_ij und δ_i bzw. δ_j entsprechen den Spannungswinkeln an den jeweiligen Netzknoten.

Die zweite implementierte Nebenbedingung ist die Nebenbedingung für die maximale Stromtragfähigkeit der Leitungen. Das Ziel der Netzausbauplanung einen engpassfreien Netzzustand bei minimalen Kosten für jeden Betriebsfall zu ermitteln. Aus diesem Grund wurde die Nebenbedingung für die maximale Stromtragfähigkeit der Leitungen implementiert. Diese Nebenbedingung bezieht sich auf den aktuellen Stromfluss I_ij über einem Zweigelement zwischen den Knoten i und j. Dieser darf den durch dieses Zweigelement maximal übertragbaren Strom I_ij^max nicht überschreiten. Da die Maßnahmen, wie sie im Rahmen der optimierten Netzausbauplanung eingesetzt werden können, einen Einfluss auf diesen maximal übertragbaren Strom haben, hängt diese Variable ebenfalls vom Entscheidungsvektor u_ij ab.

Nachfolgend sind die Nebenbedingungen der optimierten Netzbetriebsführung dargestellt:

Neben den Nebenbedingungen die in der optimierten Netzausbauplanung enthlaten sind, müssen für die netzbetrieblichen Freiheitsgrade noch die notwendigen Limitierungen und Rahmenbedingungen eingeführt werden. Die erste Nebenbedinung der optimierten Netzbetriebsfürhung beinhaltet die Bilanzaneutralität der Änderungen der Wirkleistungen an den Netzknoten. Hier spiegeln ΔP_pos,r und ΔP_neg,r die positiven als auch negativen Änderungen der Wirkleistungseinspeisung der unterschiedlichen Erzeugungs-, Verbrauchs- und Erzeugungskategorien mit Speicherfüllstandsrestriktionen wieder, welche für die optimierte Netzbetriebsführung zur Verfügung stehen.

Des Weiteren gelten für die verschiedenen Freiheitsgrade zusätzliche physikalische Limitierungen wie beispielsweise die minimale oder maximale Wirkleistungseinspeisung. Diese werden durch die oben dargstellten Nebenbedingungen in das Modell implementiert. Hier entsprechen P_min,g bzw. P_max,g den betrieblichen Grenzen hinsichtlich der Wirkleistungseinspeisung der Erzeugungsanlagen g in der Menge aller Erzeugungsanlagen G, P_min,l bzw. P_max,l den betrieblichen Grenzen hinsichtlich des Wirkleistungsbezugs der Verrbaucher l in der Menge aller Verbraucher L und P_min,g bzw. P_max,g den betrieblichen Grenzen der Erzeugungsanlagen mit Speicherfüllstandsrestirktionen s in der Menge aller Erzeugungsanlagen mit Speicherfüllstandsrestirktionen S.

Nachfolgend sind die Gleichungen sowie eine Visualisierung dieser Gelichungen gegeben, über welche die HGÜ-Verbindungen in die Optimierungsmodelle der Netzausbauplanung und Netzbetriebsführung implementiert sind:

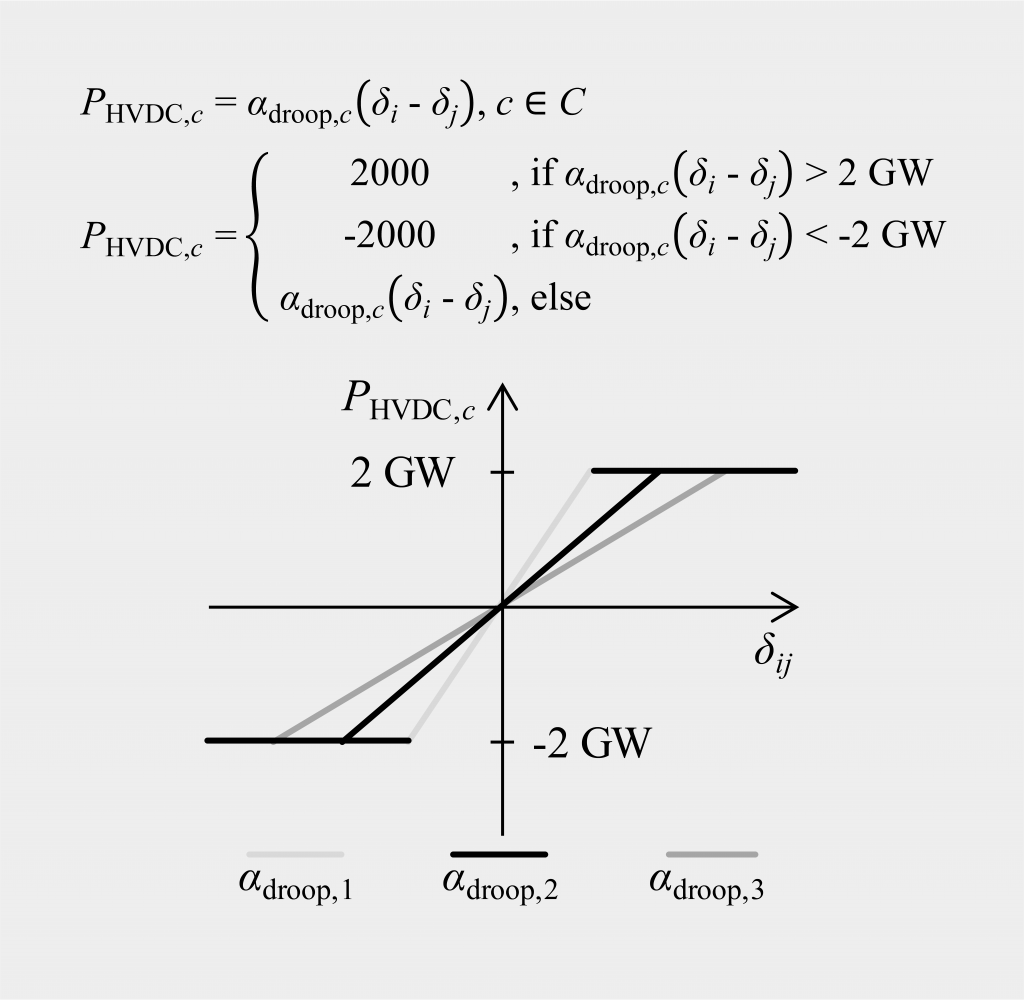
Um die HGÜ-Verbindungen in den Optimierungsmodellen zu implementieren, wurden die HGÜ-Konverter und ihre entsprechenden Arbeitspunkte über eine Droop-Regelung modelliert. Die allgemeine Formulierung dieser Regelung und der daraus resultierenden Wirkleistungseinspeisung bzw. –verbauch ist in der ersten Gleichung dargestellt. Hier sind δ_i bzw. δ_j die Knotenspannungswinkel der der AC-Netzknoten der HGÜ-Konverter. Der Droop-Faktor τ wurde basierend auf einer Leistungsflussberechnung für das gesamte Jahr sowie separat für jede HGÜ-Verbindung basierend auf der Knotenspannungswinkeldifferenz der jeweils korrespondierenden AC-Netzknoten ermittelt. Ebenfalls werden die Konveter auf eine maximale Leistung von 2 GW begrenzt.

Nachfolgend sind die Gleichungen gegeben, über welche die Speicherfüllstandsrestriktionen in das Optimierungsmodell der Netzbetriebsführung implementiert sind:

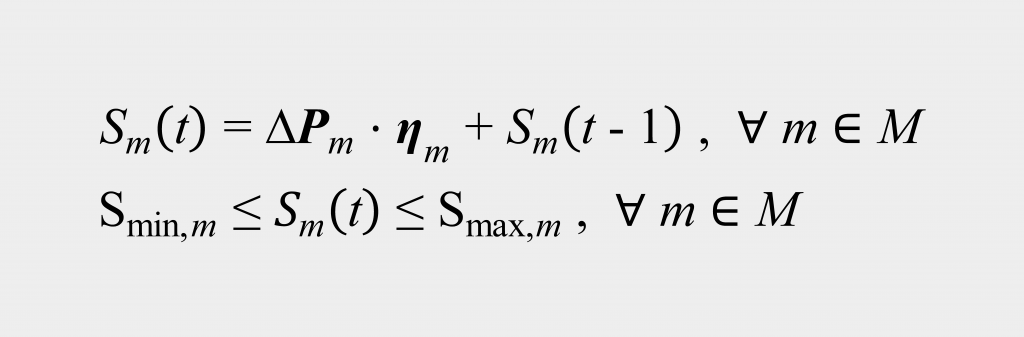
Für die unterschiedlichen Erzeugungskategorien mit Speicherfüllstandsrestriktionen die Speicherfüllstände inkl. deren Limitierungen in das Optimierungsmodell eingebunden. Diese physikalischen Gegebenheiten werden über die dargestellten Gleichungen modelliert.

Hier ist S_m(t) der aktuelle Speicherfüllstand im betrachteten Zeitschritt t, welcher zwischen dem minimalen Speicherfüllstand S_min,m(t) und dem maximalen Speicherfüllstand S_max,m(t) liegen muss. Dies gilt für alle Erzeugungskategorien mit Speicherfüllstandsrestriktionen m in der Menge aller Erzeugungskategorien mit Speicherfüllstandsrestriktionen M. Die Änderung der Wirkleistungseinspeisung bzw. des Wirkleistungsbezugs wird repräsentiert durch den Vektor:
ΔP_m = (ΔP_pos,m, ΔP_neg,m)
und die Wirkungsgrade der jeweiligen Speichertechnologien bei Einspeisungs- bzw. Verbrauchserhöhung oder –reduzierung durch den Vektor:
η_m = (η_pos,m, η_neg,m).
Um den Speicherfüllstand für den betrachteten Zeitschritt t zu bestimmen muss an dieser Stelle ebenso der Speicherfüllstand des vorherigen Zeitschritts
S_m(t – 1) basierend auf den zuvor ermittelten Ergebnissen der optimierten Netzbetriebsführung berücksichtigt werden.

Für die Untersuchungen werden drei Szenarien unterschieden:

1. Szenario „Hohe dezentrale Flexibilität“

In diesem Szenario wird angenommen, dass 60 % der Fahrzeuge ihren Ladevorgang für den Strommarkt optimal flexibel verschieben können unter perfekter Voraussicht der geplanten Wege und unter der Bedingung, dass diese ohne Einschränkung gefahren werden können. Die verbleibenden 40 % der Fahrzeuge laden ungesteuert und unmittelbar nach Ankunft an einem Ladepunkt und gehen somit als fixer Verbrauch ins Energiesystem ein. Für die dezentrale Wärmeversorgung wird durch Wärmespeicher ebenso eine Flexibilisierung des Verbrauchs ermöglicht. Unter der Annahme, dass im zukünftigen Energiesystem 60 % der Elektroautos durch Marktsignale gesteuert ihren Ladezeitraum verschieben können, werden im Energiesystem noch etwa 20 GW weitere Stromspeicher benötigt.

2. Szenario „Reduzierte Flexibilität“:

Hier wird angenommen, dass die E-Fahrzeuge ihre Last nicht verschieben können und bei der dezentralen Wärmeversorgung keine Wärmespeicher vorhanden sind. Dafür wird die Industrieflexibilität um den Faktor drei erhöht.

Dafür wird die Lastflexibilität in der Industrie um den Faktor 3 erhöht. Der Stromspeicherbedarf steigt dann in diesem Szenario auf 43 GW.

3. Szenario „Mehr Wind in Bayern“:

Dieses Szenario ist ebenfalls vom Szenario „Hohe dezentrale Flexibilität“ abgeleitet mit einer veränderten regionalen Verteilung der Windleistung mit der Annahme, dass die 10H-Regel in Bayern außer Kraft gesetzt wird und somit die installierte Windleistung in Bayern deutlich höher ist.

Nachfolgend sind die Ergebnisse des Szenarios „Hohe dezentrale Flexibilität“, welches im Rahmen des Projekts DeV-KopSys betrachtet und berechnet wurde dargestellt.

Zunächst werden dazu die Ergebnisse der einzelnen 8760 Zeitschritte (jährliche Auswertung in stündlicher Auflösung) dargestellt. Die gestapelten Balken entsprechen dabei den ausgewählten Maßnahmen für jedes Zweigelement über alle Zeitschritte. So kann es vorkommen, das für ein Zweigelement durchaus mehrere Maßnahmen gezogen werden, da dieses in den unterschiedlichen Zeitschritten und den damit einhergehenden unterschiedlichen Leistungsflusssituationen und somit auch Auslastungen hervorrufen. Die farbliche Kodierung entspricht dabei den folgenden Maßnahmen:

• Grün: Leiterseilmonitoring (LM)
• Rot: Hochtemperatur Leiterseile in Kombination mit Leiterseilmonitoring (LM + TAL)
• Blau: Wechsel des Leitungstyps zu „FL (2/4) x 450²“ in Kombination mit Leiterseilmonitoring (FL (2/4) x 450² + LM)
• Rot: Wechsel des Leitungstyps zu „FL (2/4) x 650²“ in Kombination mit Leiterseilmonitoring (FL (2/4) x 650² + LM)
• Violett: Wechsel der Spannungsebene des Zweigelements von 220 kV zu 380 kV

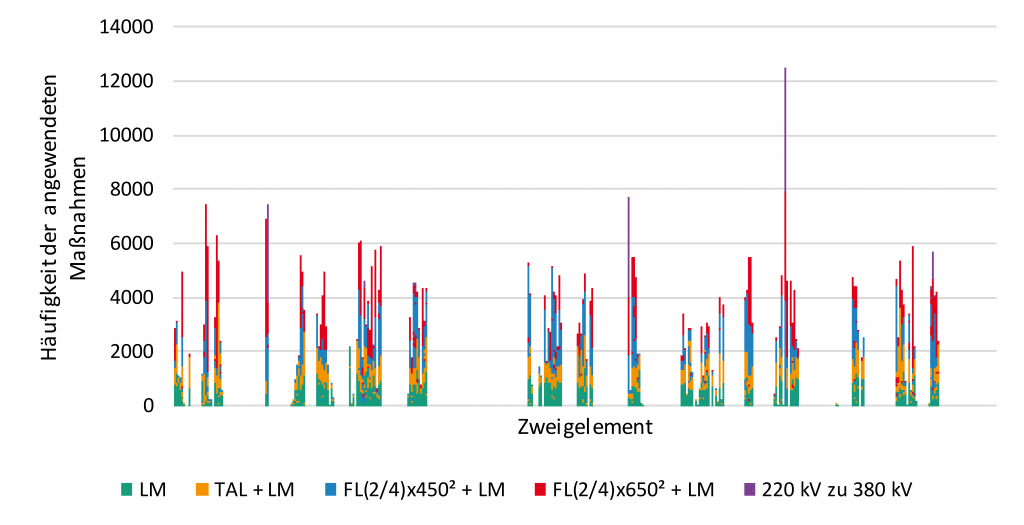
Nachdem die Ergebnisse für die einzelnen Zeitschritte durch die mathematische Optimierung berechnet wurden, müssen nun die noch finalen Ausbaumaßnahmen für die Zweigelemente bestimmt werden, welche im Anschluss das Ausgangsnetz für die optimierte Netzbetriebsführung bilden. Die finalen Entscheidungen für die jeweiligen sind in der nachfolgenden Abbildung dargestellt.

Nachdem die optimierte Netzausbauplanung durchgeführt wurde und die Maßnahmen für die jeweiligen Zweigelemente ausgewählt wurden, wird basierend auf diesen Ergebnissen die optimierte Netzbetriebsführung für jeden der 8760 Zeitschritte durchgeführt. Nachfolgend werden die Ergebnisse dieser für das Szenario „Hohe dezentrale Flexibilität“ für die jeweiligen Zeitschritte aber auch zeitschrittübergreifend für die unterschiedlichen Technologien präsentiert.

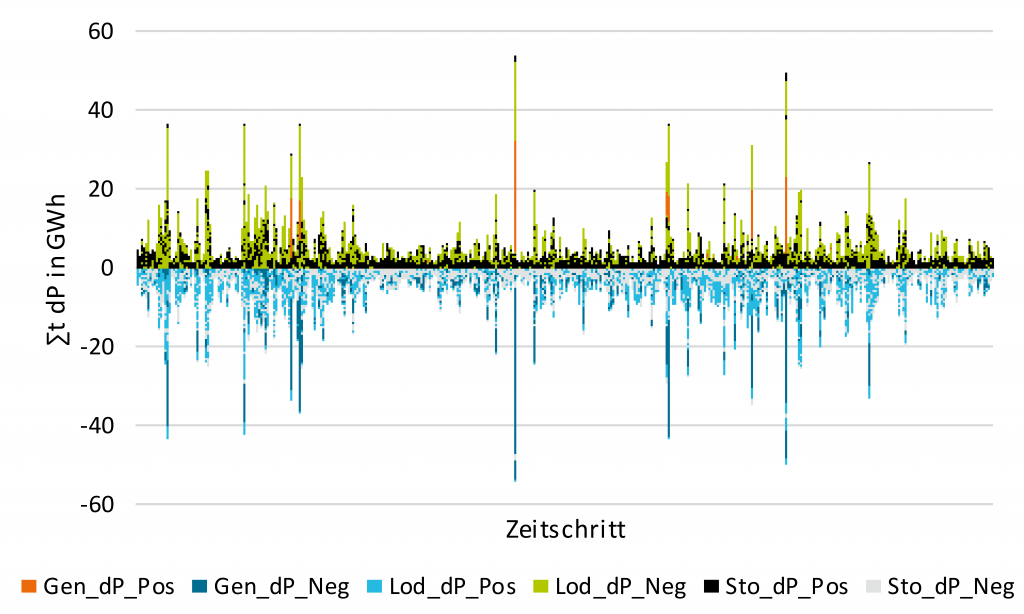
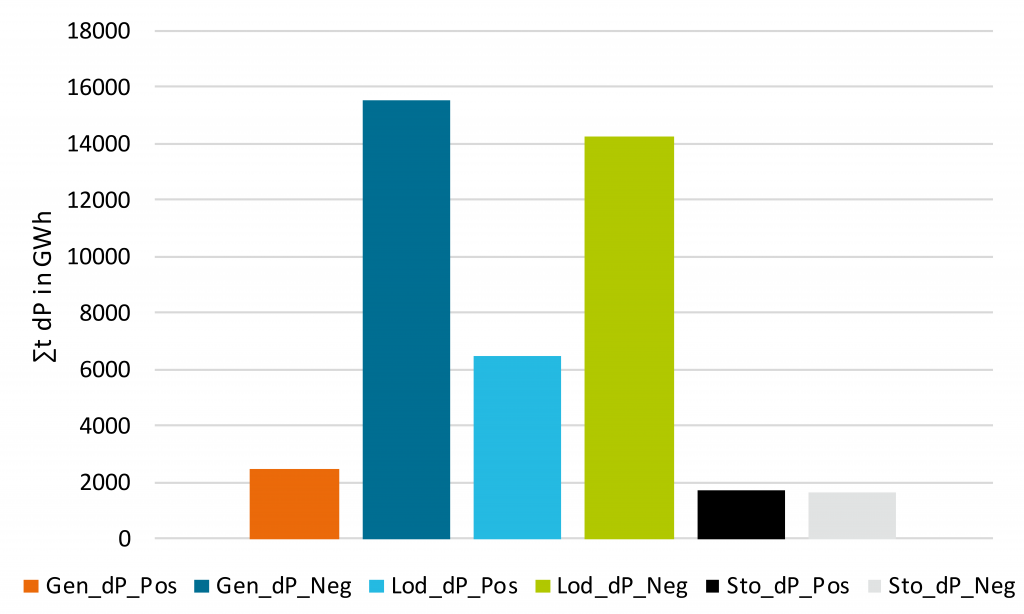
Im Mittel über alle 8760 liegen die Werte für die Einspeisungserhöhung bzw. –reduzierung bei 0,28 GWh bzw. 1,78 GWh, für die Verbrauchserhöhung bzw. –reduzierung bei 0,74 GWh bzw. 1,63 GWh und für die Leistungsanpassung der Technologien mit Speicherfüllstand bei 0,19 GWh für die Erhöhung der Leistung und 0,19 GWh für die Reduzierung der Leistung. Um einen Überblick über die Jahressummen zu erhalten, sind diese noch einmal in der nachfolgenden Grafik dargestellt aufgeteilt nach Erzeugungserhöhung (Gen_dP_Pos), Erzeugungsreduzierung (Gen_dP_Neg), Verbrauchserhöhung (Lod_dP_Pos), Verbrauchsreduzierung (Lod_dP_Neg), Leistungserhöhung für Technologien mit Speicherfüllstand (Sto_dP_Pos) und Leistungsreduzierung für Technologien mit Speicherfüllstand (Sto_dP_Neg).